Nadszedł na blogu sądny dzień. Zabieramy się bowiem za chyba najstraszniejszy w obiegowej opinii temat jakim jest niepewność pomiarów. W mojej ocenie temat ten odbierany jest jako straszydło w większości przedsiębiorstw, w zasadzie poza laboratoriami pracującymi według wytycznych ISO/IEC 17025, gdzie z konieczności trzeba było zagadnienie zrozumieć i wdrożyć. I chyba właśnie zaistnienie konieczności obliczania niepewności jest kryterium decydującym o zmianie podejścia wobec tego zagadnienia. Dopóki nie musimy tego robić, niepewność pomiaru majaczy gdzieś w oddali, a użytkownicy mają nadzieję, że zdążą doczekać do emerytury zanim ktoś zacznie od nich tego wymagać. I można by takie podejście próbować zrozumieć gdyby można było zakwalifikować kwestię niepewności pomiaru jako rzecz opcjonalną, nie dotyczącą wszystkich uczestników procesów pomiarowych. Tyle, że tak nie jest…

Problem z niepewnością zaczyna się niestety właśnie w podejściu, za co pośrednio winić należy „system” kształcenia. O tym, jak bardzo trudne czy wręcz niepoliczalne jest to zjawisko krążą legendy. Wizja wykonywania nieskończenie długich obliczeń i stosowania wzorów, które rozumieją tylko laureaci nagrody Nobla w dziedzinie matematyki jest dla wielu pomiarowców odpychająca. Tyle, że tak być nie musi…

Czasy wykonywania żmudnych obliczeń (najlepiej na papierze, z kalkulatorem) minęły. Dysponujemy całą gamą narzędzi, które mogą ułatwić i zautomatyzować proces szacowania niepewności pomiaru. Mając na uwadze powyższe podejmę się zadania wprowadzenia Was w świat niepewności pomiaru w sposób tak przystępny, jak tylko się da. W tym celu – uprzedzam czepialskich – posłużę się kilkoma uproszczeniami, porównaniami i niewyszukanym słownictwem. Mam nadzieję, że pozwoli Wam to wreszcie zrozumieć to zagadnienie i odważnie stawić mu czoła. Wszystkie uproszczenia pozwolę sobie „uprofesjonalnić” i wyprostować w kolejnych częściach artykułu.

W niniejszej, pierwszej części zajmiemy się udzieleniem odpowiedzi na najważniejsze pytania i obalimy kilka błędnych lub mylących twierdzeń na temat niepewności pomiaru. Do dzieła!

Źrodła i dokumenty

Z szacowaniem i wyrażaniem niepewności w pomiarach i wzorcowaniach związanych jest sporo dokumentów w postaci przewodników i norm. Poniżej przytaczam te najważniejsze i polecane przeze mnie.

1. JCGM 100:2008 -Ewaluacja danych pomiarowych. Przewodnik wyrażania niepewności pomiaru. Międzynarodowy przewodnik wydany przez JCGM ma charakter uniwersalny i jest podstawowym dokumentem stosowanym przez laboratoria na całym świecie. UWAGA: Aktualne wydanie jest dostępne jako PKN-ISO/IEC Guide 98-3:2021-05. Niepewność pomiaru — Część 3: Przewodnik wyrażania niepewności pomiaru (GUM:1995), wraz z dokumentami uzupełniającymi jak np. PKN-ISO/IEC Guide 98-1:2021-06 – Niepewność pomiaru — Część 1: Wprowadzenie do wyrażania niepewności pomiaru oraz ISO/IEC Guide 98-4:2012 Uncertainty of measurement — Part 4: Role of measurement uncertainty in conformity assessment.
2. EA-4/02 M:2022 -Ocena niepewności pomiaru przy wzorcowaniu – dokument dedykowany dla laboratoriów wzorcujących. To według jego wytycznych podawana jest niepewność pomiaru na świadectwach wzorcowania, które otrzymujecie z laboratorium.
3. IEC Guide 115, Application of uncertainty of measurement to conformity assessment activities in the electrotechnical sector – przewodnik dedykowany dla branży elektrotechnicznej wyróżnia się przejrzystością i zrozumiałymi przykładami.
4. PN-EN ISO 14253-2:2011 – Specyfikacje geometrii wyrobów (GPS) — Kontrola wyrobów i wyposażenia pomiarowego za pomocą pomiarów — Część 2: Wytyczne szacowania niepewności pomiarów w GPS, przy wzorcowaniu wyposażenia pomiarowego i sprawdzaniu wyrobów. Ta i kolejne normy z tej „podrodziny” aż po 14253-5 są wartymi zainteresowania normami o charakterze nieco bardziej praktycznym i „produkcyjnym” w odróżnieniu od przytoczonych wyżej mocno laboratoryjnych

Czym jest niepewność pomiaru?

Chcąc zachować wspomnianą we wstępie prostotę będę trzymał się możliwie z dala od niezrozumiałych dla laika definicji, którymi częstują nas przewodniki. Moim zdaniem najbardziej przemawiająca do wyobraźni definicja niepewności pomiaru brzmi:

Symetryczny przedział wokół wartości zmierzonej (wyniku pomiaru), w którym z określonym prawdopodobieństwem zawiera się wartość rzeczywista.

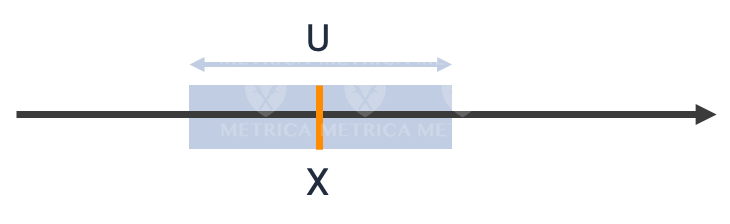
Zakładam, że moi czytelnicy są już świadomi tego, że wynik pomiaru nie jest pojedynczą wartością. Jest przedziałem, czy też w pewnym przedziale się zawiera. Szerokość tego przedziału to właśnie niepewność pomiaru.

Czym niepewność pomiaru nie jest?

Spotykam się z kilkoma niewłaściwymi interpretacjami niepewności pomiaru, które wyjaśniam poniżej.

Niepewność pomiaru to nie błąd pomiaru (czy też błąd wskazana przyrządu).

Niepewność z błędem jest oczywiście związana, ale mówi nam raczej o tym (uwaga) z jakim błędem (niedokładnością) ów błąd został wyznaczony. Przy czym przedział niepewności zawiera w sobie znacznie więcej niż tylko sam błąd. Normalną sytuacją jest, że błąd ma wartość zero, ale niepewność pomiaru już nie. Zresztą niepewność wynosząca zero nie jest możliwa do uzyskania. W naszej rzeczywistości nie istnieje proces pomiarowy bezbłędny…

Po drugie:

Niepewność pomiaru podana na świadectwie wzorcowania czy pomiaru nie mówi o tym jaką niepewność w pomiarach przyrządem uzyska użytkownik.

Mówi natomiast o tym, z jaką „niedokładnością” laboratorium podane wartości błędów uzyskało w swoich warunkach, swoim wyposażeniem, zastosowaną metodą. Wartości niepewności, jakie uzyskuje laboratorium określane są przez tzw. CMC (ang. calibration and measurement capability) – zdolność pomiarowa laboratorium. Nota bene wartość CMC jaką uzyskuje laboratorium, któremu zamierzamy zlecić usługę wzorcowania można wygodnie sprawdzić w zakresie akredytacji laboratorium, do wglądu na stronie pca.gov.pl. Ma to niebagatelne znaczenie w sytuacji, w której zależy nam na uzyskaniu jak najniższej niepewności aby umożliwić sobie właściwą ocenę zgodności. O tym będzie jednak później.

O czym mówi niepewność pomiaru?

Niepewność pomiaru odzwierciedla łączny wpływ wszystkich czynników, które miały wpływ na uzyskany wynik pomiaru lub wzorcowania. Czynniki te nazywamy składowymi niepewności. Składowe niepewności mają różne źródła, podobnie jak na każdy wykonywany przez nas pomiar wpływa wiele czynników. Szerzej o źródłach błędów opowiem w innym wpisie, tu zamieszczę tylko tabelę z podziałem na 7 kategorii zakłóceń pomiaru z kilkoma przykładami:

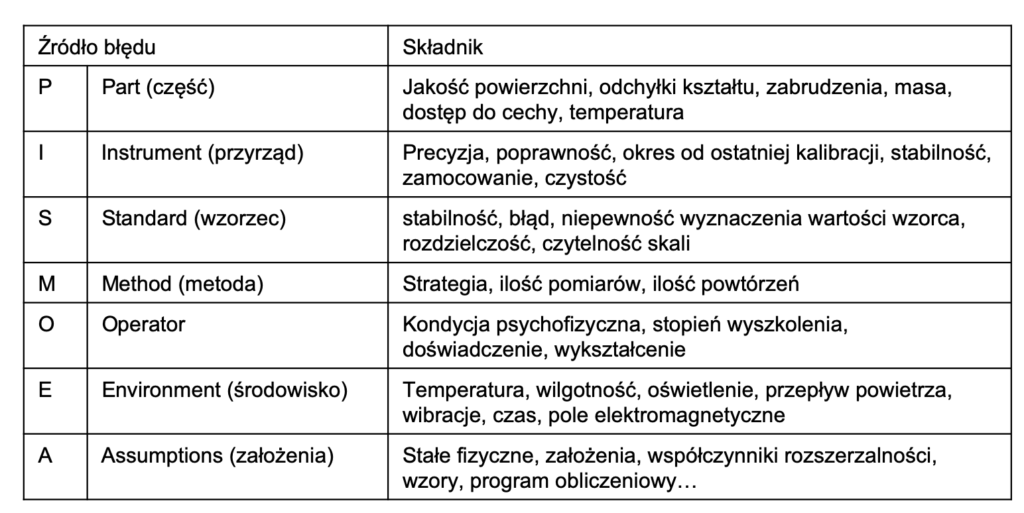
Nie ma zmiłuj, mniej lub bardziej wszystkie wymienione wyżej składniki wpływają na każdy pomiar, a niepewność pomiaru stara się ten wpływ określić. Na podstawie zdobytej już wiedzy możemy sformułować następujący wniosek:

Niepewność pomiaru odzwierciedla jakość pomiaru.

Jak interpretować niepewność pomiaru?

Jak wspomnieliśmy wyżej, wynik pomiaru uznać możemy za kompletny jeśli został podany wraz z rozszerzoną niepewnością pomiaru. Ta z kolei oszacowana została z pewnym poziomem ufności. Zgodnie z dokumentem EA-4/02 laboratoria zobligowane są do podawania na świadectwach następującej formuły:

Niepewność pomiaru została określona zgodnie z dokumentem EA-4/02 M:2022. Podane wartości niepewności stanowią niepewności rozszerzone przy prawdopodobieństwie rozszerzenia ok. 95 % i współczynniku rozszerzenia k = 2.

Jeśli zatem przedmiotem rozważania jest świadectwo wzorcowania, na którym podano np., że błąd wskazania w punkcie x wynosi + 0,01 mm z niepewnością 0,01 mm, to należy rozumieć ten zapis następująco:

Wartość błędu wskazania w tym punkcie zawiera się w przedziale od 0,00 do 0,02 mm, z prawdopodobieństwem 95%.

Jeśli błąd wskazania wynosi „0”, z niepewnością +/- 0,003 mm, to rzeczywisty błąd znajduje się w przedziale od -0,003 do 0,003 mm.

Analogicznie jeśli wyniki podawane są w wartościach względnych. Niepewność pomiaru wynosząca 5% oznacza, że wartość rzeczywista znajduje się w przedziale +/- 5% od wartości zmierzonej.

Po co szacować i podawać niepewność pomiaru?

Bez podanej niepewności pomiaru niemożliwa jest właściwa ocena o zgodności wyrobu czy narzędzia ze specyfikacją. W profesjonalnej metrologii, na poziomie laboratoryjnym, wynik pomiaru bez rozszerzonej niepewności pomiaru jest bezużyteczny. Dlaczego?

Twierdzenie, że pomiar bezbłędny nie istnieje, automatycznie implikuje kolejne, mianowicie: każdy pomiar obarczony jest błędem. Jeśli błąd ten jest nieznany, a więc nie wiemy jaka jest szerokość przedziału, w którym znajduje się wartość rzeczywista, to znaczy, że generalnie wartość rzeczywista może przyjąć dowolną wartość (oczywiście w uproszczeniu – gdy poznamy rozkłady prawdopodobieństwa twierdzenie to będzie można wyprostować…).

Jak oblicza się niepewność pomiaru?

Szacowanie niepewności pomiaru to analityczny proces, którego najtrudniejszą częścią nie są wcale same obliczenia.

Najtrudniejszym elementem szacowania niepewności pomiaru jest rzetelna i właściwa identyfikacja składników, a więc wszystkich czynników wpływających na pomiar.

Proces szacowania niepewności nigdy nie kończy się „oszacowaniem na 100%”, wciąż poruszamy się w pewnych przybliżeniach. Niemniej w zależności od współczynnika rozszerzenia osiągamy zwykle przedział ufności rzędu 95, a nawet 99,7%.

Obliczanie niepewności pomiaru to proces składający się z 4 etapów:

1. W pierwszym kroku należy zidentyfikować wszystkie wpływające na proces pomiarowy czynniki – składowe niepewności pomiaru (Xn). I tu właśnie pojawia się pytanie – czy jesteśmy w stanie oszacować je wszystkie? Niestety nie…
2. W drugim sporządzamy tzw. budżet niepewności, będący uporządkowaną tabelą, w której dla zidentyfikowanych składowych oszacujemy estymaty lub granice zmienności, i obliczymy ich udział w niepewności standardowej złożonej (u_x). Estymata to oszacowana wartość danej wielkości wpływającej. Czasem zamiast estymaty podaje się granice zmienności (np. granice błędu dopuszczalnego przyrządu). O tym, co odróżnia oba podejścia opowiem w kolejnym wpisie.
3. W trzecim obliczymy niepewność standardową złożoną (u) jako pierwiastek sumy kwadratów niepewności składowych.
4. W czwartym wreszcie wyznaczymy niepewność rozszerzoną (U) będącą iloczynem niepewności standardowej złożonej (u) i współczynnika rozszerzenia (k). Współczynnik rozszerzenia przyjmuje najczęściej wartość 2 lub rzadziej (przynajmniej w metrologii długości i kąta) 3. W praktyce jeśli wartości zmierzone charakteryzują się rozkładem normalnym przyjmuje się k=2.

Mam nadzieję, że się nie pogubiliście… Celowo nie będę rozwijał tu szczegółów, bo proces sporządzania budżetu i szacowania niepewności to temat części drugiej. Odpowiem jednak na istotne dla zrozumienia pytanie, które może zadać spostrzegawczy czytelnik, mianowicie: skoro zależy nam na jak najmniejszej niepewności, to dlaczego mnożymy uzyskaną niepewność złożoną x2 lub nawet x3? Przecież powiększamy w ten sposób przedział dwu- lub trzykrotnie! Gdzie sens i logika?

Odpowiadam: zależy nam, aby mieć jak największą pewność, że wynik pomiaru znajduje się w obliczonym przez nas przedziale. Jaki poziom ufności uzyskalibyśmy bez pomnożenia niepewności złożonej przez (k)? Raptem około 68%… Bezpieczeństwo decyzji przede wszystkim!

Gdzie ta matematyka?

W zmaganiach z niepewnością pomiaru naszymi najważniejszymi narzędziami będą średnia arytmetyczna i odchylenie standardowe.

Powinniście już wiedzieć, że wykonując serię powtórzeń w tych samych warunkach (tzw. warunkach powtarzalności), może zdarzyć się tak, że każdy uzyskany wynik będzie inny. I nic w tym dziwnego – jeden pomiar, to nie pomiar, a każdy poważny metrolog wie, że wynikiem jest średnia z serii pomiarów.

Odchylenie standardowe natomiast jest podstawową miarą rozrzutu. W niektórych przypadkach stosuje się dodatkowo lub zastępczo rozrzut wartości w serii pomiarów, który jest różnicą między wartością MAX a MIN. Miara ta na potrzeby analiz statystycznych jest jednak obarczona istotną wadą – pojedyncza wartość mocno odstająca od średniej nadmiernie rozrzut powiększa.

Samo odchylenie standardowe jest miarą precyzyjniejszą. Mówi nam, jak bardzo wartości w serii pomiarów różnią się od wartości średniej. Odchylenie standardowe z definicji jest pierwiastkiem kwadratowym z wariancji, bo może brzmieć strasznie, w praktyce wcale takim nie jest – poradzimy sobie z jego obliczaniem bez problemu Excelem, czasem kalkulatorem, a od biedy i na papierze.

Na dziś to tyle. Chciałbym, żebyście oswoili się z powyższymi konceptami i terminami, aby przygotować w Waszych głowach żyzną glebę dla informacji, które szykuję w kolejnych częściach niniejszego cyklu. Jak zwykle zapraszam do kontaktu i zadawania pytań, a jeśli temat niepewności pomiaru podchodzi już pod bramy Twojego zakładu pracy i nie czujesz się na siłach ogarnąć go samodzielnie – zapraszam na moje szkolenia i współpracę w zakresie bezbolesnego wdrożenia omawianego procesu.