Płytki interferencyjne. Pomiary płaskości małych powierzchni metodą interferencyjną.
Witam po raz pierwszy w 2026 roku!
Po ostatnim dość ciężkim temacie dla kontrastu dziś mam dla Was wpis zdecydowanie bardziej praktyczny. Będzie można ładne rzeczy pooglądać, dzięki czemu pokażemy piękniejszą stronę metrologii. Bohaterkami dzisiejszego posta będą bowiem płytki interferencyjne, a ja opowiem jak wykorzystać je w pomiarach płaskości małych, precyzyjnych powierzchni.
Temat niejako kontrastuje z opublikowanym jakiś czas temu materiałem na temat pomiarów płaskości w dużej skali. Również bazuje na tradycyjnej warsztatowej metodzie, której zastąpienie jest wprawdzie możliwe, ale często ekonomicznie nieuzasadnione, a którą to każdy szanujący się metrolog powinien znać.
Płaskość w mikroskali
Skoro o płaskości w dużej skali na blogu było, skupmy się teraz na płaskości w skali mikro. Charakterystyka ta ma znaczący wpływ na trwałość i funkcjonalność wielu komponentów i ich połączeń. Skala, o której obecnie mówimy wymaga niejednokrotnie badania odchyłek w dziesiętnych częściach mikrometra, czy może już lepiej powiedzieć – w nanometrach. Gdzie zatem występują takie wymagania?
| Zastosowanie | Dlaczego to ważne? | Potencjalne problemy |
| Elementy Uszczelniające (np. uszczelnienia mechaniczne) | Zapewnienie ciągłej, jednorodnej powierzchni styku. | Wycieki medium, przedwczesne zużycie, przegrzewanie. |
| Łożyska i Powierzchnie Prowadzące | Równomierny rozkład obciążenia, minimalizacja tarcia i zużycia. | Nierównomierne obciążenie, wibracje, utrata precyzji ruchu. |
| Optyka Precyzyjna (lustra, płytki światłowodowe) | Minimalizacja aberracji, zachowanie jakości i spójności wiązki światła. | Zniekształcenie obrazu |
| Płytki wzorcowe | Podstawowe wzorce długości stosowane w metrologii | Błędy w kalibracji innych narzędzi pomiarowych |
| Powierzchnie pomiarowe innych urządzeń pomiarowych, np. mikrometru | Aby osiągnąć zdolność pomiarową w tysięcznych częściach mm, komponenty wpływające muszą być precyzyjne | Nadmierne błędy przyrządów pomiarowych |
Problemy związane z pomiarami mającymi na celu weryfikację spełnienia tych wymagań są generalnie dwa: wymaganie jest wysokie, powierzchnia natomiast bardzo mała.
Niech za przykład reprezentatywny posłuży nam płaska powierzchnia pomiarowa mikrometru zewnętrznego (wprawdzie już nie jest w normie tolerowana bezpośrednio, ale przykład jest idealny). Zadanie polega na wyznaczeniu odchyłki od płaskości powierzchni o średnicy 6 lub 8 mm, dla której wymaganie płaskości wynosi 0,6 mikrometra. Dodatkowo płaszczyzna nie jest w pełni eksponowana, bo na dostęp do niej zostaje nam ok. 25 mm. Na wstępie musimy odrzucić cały arsenał sprzętów, które nie są w stanie zejść poniżej mikrona, w tym także stosowane szeroko do pomiaru płaskości maszyny współrzędnościowe. Co zostaje? Garstka komparatorów czujnikowych i czujników indukcyjnych, których zdolność pomiarowa jest wystarczająca, ale z racji ograniczonego dostępu do cechy zastosować ich nie sposób.
Dlatego też standardem w tym i podobnych zastosowaniach są od lat płytki interferencyjne, a więc bardzo precyzyjne wzorce płaskości i/ lub także równoległości.
Płytki interferencyjne – opis i rodzaje
Płytka interferencyjna (nazywana też płaską szklaną) to precyzyjny krążek wykonany ze szkła optycznego (BK7) lub kwarcu. Przynajmniej jedna z jego powierzchni (powierzchnia robocza) jest wzorcem płaskości. Jeżeli jest to tylko jedna płaszczyzna (wskazana strzałką), to płytkę taką nazywamy płaską jednostronną, jeżeli natomiast wzorcowe są obie – dwustronną.
Płytki wykonywane są według niemieckiego standardu DIN 51861 w dwóch wersjach:
- Testing of optical components – Part 1: Test glasses with flat surface (płytki z powierzchniami płaskimi)
- Testing of optical components – Part 2: Test glasses with spherical surface (płytki z powierzchniami sferycznymi)
Płytki interferencyjne są zazwyczaj okrągłe. Ich średnica musi być dobrana tak, aby pokrywała w całości badaną powierzchnię. Grubość płytki również jest istotna, aby zapobiec jej odkształceniom pod wpływem własnego ciężaru lub nacisku.
- Spotykane średnice: 30, 45, 60, 80, 100, 125, 150, 200 i więcej – nawet 600 mm.
- Grubość: Zazwyczaj od 10 mm do 30 mm

Dokładność płytek określa się w klasach (zazwyczaj 1 i 2, rzadziej klasa 0…). Odchyłka płaskości podawana jest w mikrometrach i odnosi się do maksymalnej odchyłki całej powierzchni powierzchni. Zestawienie odchyłek dopuszczalnych dla typowych wymiarów płytek poniżej.
Zwracam uwagę, że w niektórych opracowaniach możecie spotkać się z dopuszczalną odchyłką płytki wyrażoną jako np. λ/10. Oznacza to 0,03 mikrometra a już za chwilę dowiecie się dlaczego.
| Średnica nominalna (mm) | Typowa grubość (mm) | Dopuszczalna odchyłka płaskości – Klasa 1 (μm) | Dopuszczalna odchyłka płaskości – Klasa 2 (μm) |
| 30 | 10 – 12 | 0,03 | 0,1 |
| 45 | 10 – 12 | 0,03 | 0,1 |
| 60 | 15 | 0,03 | 0,1 |
| 80 | 15 – 20 | 0,03 | 0,1 |
| 100 | 20 – 25 | 0,05 | 0,12 |
| 125 | 25 | 0,05 | 0,12 |
| 150 | 30 | 0,05 | 0,12 |
| 200 | 35 – 40 | 0,1 | 0,25 |
Jak to działa?
Metoda pomiaru płaskości za pomocą płytek interferencyjnych wykorzystuje zjawisko interferencji fal światła i opiera się na zasadzie działania interferometru Fizeau, który w tym konkretnym zastosowaniu wykorzystuje zjawisko interferencji w cienkim klinie powietrznym. Jest to bezkontaktowa technika pomiarowa, która pozwala na wizualizację i ilościową ocenę odchyłek od płaskości z wysoką dokładnością.
Interferencja w różnych odmianach wykorzystywana jest w dedykowanych urządzeniach takich jak klasyczny mikroskop interferencyjny produkcji ZEISS JENA czy najdokładniejsze produkowane obecnie urządzenia do pomiaru długości jakimi są interferometry laserowe, stosowane choćby do kalibracji maszyn współrzędnościowych.

W przypadku urządzeń dedykowanych lustro wbudowane jest w obiektyw lub korpus, nie ma bezpośredniego styku płytki szklanej z obiektem, jak w metodzie omawianej we wpisie. Do obserwacji zjawiska interferencji tak czy inaczej niezbędne jest spełnienie dwóch podstawowych warunków:
1.Światło powinno być monochromatyczne: użycie światła o jednej, ściśle określonej długości fali λ, np. światła sodowego λ ≈ 589 nm ≈ 0,6 mikrona lub lampy helowej. Jest to konieczne do uzyskania wysokiej spójności czasowej, co umożliwia stabilną i wyraźną interferencję. Na rynku dostępne są monochromatyczne źródła światła pozwalające uzyskać optymalne warunki do kontroli.

2.Interferencja fal odbitych: Światło monochromatyczne pada na układ i ulega rozszczepieniu na dwie wiązki:
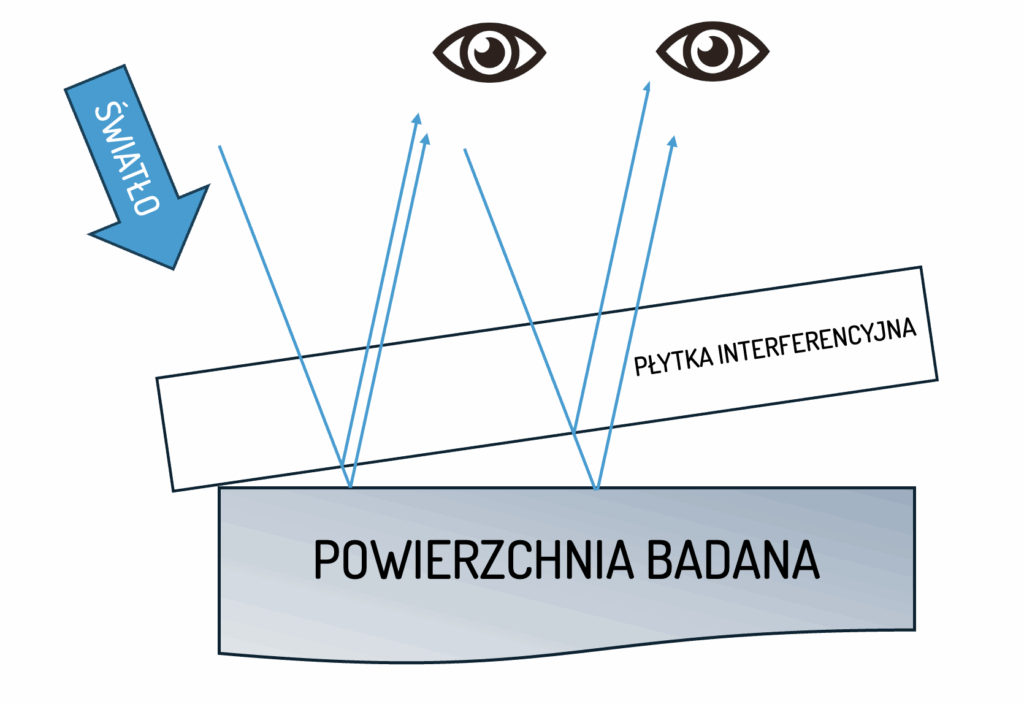
- Wiązka 1: Odbija się od dolnej powierzchni płytki szklanej wzorcowej (powierzchnia odniesienia).
- Wiązka 2: Przechodzi przez płytkę wzorcową i odbija się od górnej powierzchni badanej próbki.
Obie te wiązki są spójne (pochodzą z tego samego źródła) i po opuszczeniu układu nakładają się na siebie, tworząc zjawisko interferencji.
Wynik interferencji (jasny lub ciemny prążek) zależy od różnicy dróg optycznych ΔL przebytych przez wiązki. Różnica ta jest ściśle związana z grubością klina powietrznego g w danym punkcie. Ponieważ światło musi przebyć grubość klina dwukrotnie (w dół i w górę), różnica dróg optycznych wynosi w przybliżeniu: ΔL ≈ 2g
- Gdy fale nakładają się na siebie (są w fazie), zachodzi Interferencja konstruktywna (prążek jasny): Pojawia się w miejscach pośrednich, gdzie różnica dróg jest parzystą wielokrotnością połówek długości fali, co sprawia, że fale są zgodne w fazie
- Gdy fale znoszą się (są w przeciwfazie), zachodzi interferencja destruktywna (prążek ciemny): Powstaje, gdy różnica dróg przebytych przez dwa promienie wynosi dokładnie połowę długości fali (λ/2) lub jej nieparzystą wielokrotność (np. 3λ/2). Wówczas następuje całkowite wygaszenie światła
Ponieważ grubość klina powietrznego zmienia się w zależności od kształtu badanej powierzchni, prążki interferencyjne stanowią odwzorowanie – mapę konturową tej powierzchni. Każdy sąsiedni prążek (np. jasny) odpowiada zmianie grubości klina o dokładnie (λ / 2). Jest to podstawowa zasada, która pozwala na ilościową ocenę odchyłek od płaskości. W świetle białym lub pomarańczowym (stosowanym np. w specjalnych urządzeniach do oceny prążków) odstęp między dwoma sąsiednimi prążkami tego samego koloru oznacza zmianę odległości (szczeliny) między płytką a przedmiotem o połowę długości fali światła (λ / 2).
Tyle podstaw metody stosowanej w interferometrach. My jednak dziś nie będziemy posługiwali się interferometrem, a jedynie płytką i nieuzbrojonym okiem. W naszej warsztatowej metodzie płytka jest delikatnie przykładana do powierzchni badanej. Ze względu na nieidealną płaskość obu elementów (lub celowe minimalne pochylenie), między dolną powierzchnią płytki wzorcowej a górną powierzchnią badanego elementu powstaje cienka warstwa powietrza o zmiennej grubości, zwana klinem powietrznym. Grubość tego klina jest zazwyczaj bardzo mała, rzędu kilku długości fali świetlnej.
Odchyłkę od płaskości wyznacza się ze wzoru:
h = (λ / 2) · (Δx / x)
Gdzie:
- h – odchyłka od płaskości.
- λ – długość fali światła (np. 589 nm, najczęściej przyjmujemy 0,6 um).
- Δx – ugięcie prążka.
- x – odstęp między prążkami.
Przykład obliczeniowy: h = (589 nm / 2) · (1/4) = 294,5 nm · 0,25 ≈ 73,6 nm ≈ 0,7 um
Po uproszczeniu: 0,3 x 0,25 = 0,75 um
Wyznaczanie odchyłki w praktyce
Sam proces postępowania jest stosunkowo prosty. Tym co wymaga praktyki i na początku bywa nieintuicyjne jest wprawne ułożenie płytki i nauczenie oka szybkiej oceny ugięcia prążków. Zobaczmy więc, czy uda nam się to zrozumieć i zastosować w praktyce. Sprawę powinna ułatwić poniższa ściąga:
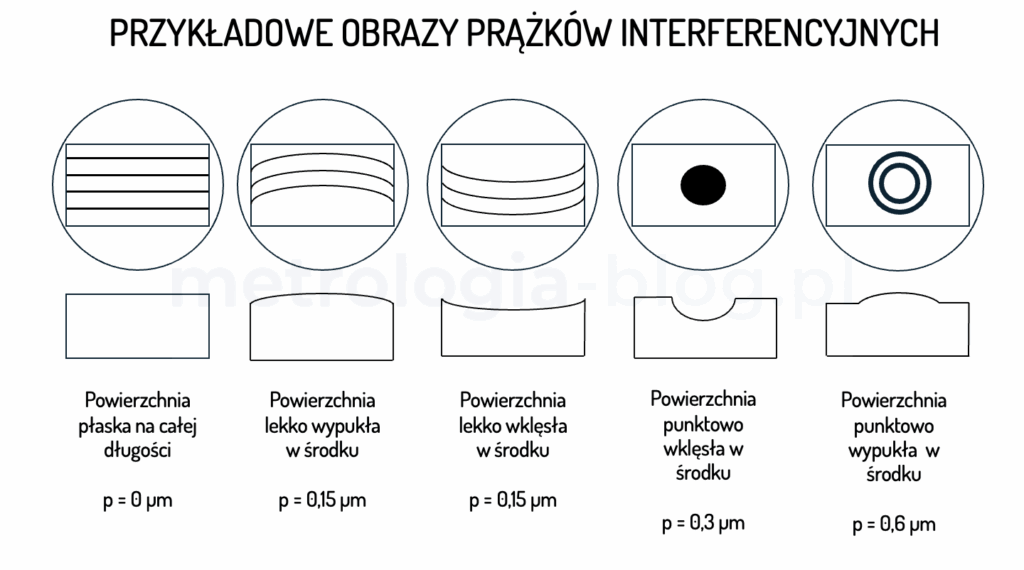
- Pierwszym krokiem jest dokładne wyczyszczenie układu pomiarowego, a więc powierzchni badanej i wzorcowej. Tłuszcz, pyłek, brud – nie muszę przypominać jak duże ma to znaczenie w naszej skali…
- Następnie przykładamy delikatnie płytkę do powierzchni badanej. Nie staraj się jej przywierać! Szklany wzorzec jest niebywale delikatny, uważaj żeby nie porysować ani nie upuścić. UWAGA! jeśli po przywarciu np. do płytki wzorcowej płytka szklana nagle odrywa się, oznacza to obecność zadzioru. Nie próbuj ponownie, grozi to porysowaniem wzorca…
- Podstawą dobrej oceny jest zachowanie klina, co wymusza nierównoległe, lekko nachylone względem badanej powierzchni ułożenie wzorca jeśli odchyłka jest niewielka (widzimy linie a nie okręgi). To najtrudniejsza część procesu wymagająca wprawy. Możesz się natknąć na warsztatowe rady takie jak „pomiar na bibułkę”, które zalecają podłożenie z jednej strony czegoś cienkiego. Idealnie jeśli klin będzie miał kilka-kilkanaście mikronów w szerszym miejscu – spróbuj na szczelinomierzu taśmowym 5 um. Wypracuj taką technikę, aby uzyskać 3-5 wyraźnych prążków co ułatwi ocenę.
- Obserwuj obraz prążków zmniejszając i delikatnie zwiększając kąt między podstawą płytki szklanej a badaną powierzchnią. Znajdź taki obraz prążków, który pozwoli Ci na skuteczną ocenę – jeśli prążki tworzą linie (nie plamy ani okręgi), będziemy musieli ocenić ich ugięcie. Obraz prążków będzie się zmieniał, ale relacja między prążkami powinna zostać zachowana – wybierz więc taki obraz, w którym prążków jest niewiele. Jeśli poruszając płytką możesz znaleźć taki obraz, że pojawia się plama (okrąg) – złap go. Wychwycisz w ten sposób największą odchyłkę.
- Jeśli nie widzisz prążków masz do czynienia z powierzchnią idealnie płaską. Albo przeciwnie – powierzchnia nie jest na tyle precyzyjnie wykończona aby zobaczyć obraz prążków, ale to powinieneś wiedzieć na starcie.
- Jeżeli zidentyfikowałeś prążki jako linie, to masz do dyspozycji dwie drogi postępowania:
- Pierwsza: metoda najbardziej u nas rozpowszechniona – dokonujemy oceny ugięcia prążków do odległości między nimi. Gdy linie są idealnie równoległe do siebie oraz proste i równo rozmieszczone, masz do czynienia z idealną płaszczyzną. Ściślej: niewielką odchyłką od płaskości, poniżej 0,1 mikrona, w zasadzie w granicach błędu pomiaru. Najczęściej w takich sytuacjach oceniam w stylu: 0,1 x 0,3 = 0,03 um.
- Jeżeli prążki są bardziej zakrzywione, powiedzmy w strefie od 1/3 do 1 odległości między nimi, dokonaj obliczenia zgodnie z ocenionym ugięciem:
- 0,3 (ugięcie na 1/3 odległości między prążkami) x 0,3 = 0,09 um
- 0,5 (ugięcie do połowy) x 0,3 = 0,15 um
- 0,7 x 0,3 = 0,21 um
- 1 x 0,3 = 0,3 um
- Jeżeli prążki są bardziej zakrzywione, powiedzmy w strefie od 1/3 do 1 odległości między nimi, dokonaj obliczenia zgodnie z ocenionym ugięciem:
- Druga: metoda z przecięciem prążków linią. Poprowadź w wyobraźni (lub przyłóż linijkę czy inną krawędź jeśli masz dostatecznie dużo miejsca) linię przez środek obrazu. Ile prążków przecina? Pomnóż ilość przeciętych prążków przez 0,3 aby uzyskać odchyłkę w mikronach zgodnie z zasadą, że 1 prążek to 0,3 mikrona.
- Jeżeli prążki są pełne – tworzą plamy lub okręgi, sprawa jest łatwiejsza. Nie ma ugięcia do oceny, liczymy jedynie widoczne prążki i mnożymy ich ilość x 0,3 i otrzymujemy odchyłkę w mikrometrach.
- Pierwsza: metoda najbardziej u nas rozpowszechniona – dokonujemy oceny ugięcia prążków do odległości między nimi. Gdy linie są idealnie równoległe do siebie oraz proste i równo rozmieszczone, masz do czynienia z idealną płaszczyzną. Ściślej: niewielką odchyłką od płaskości, poniżej 0,1 mikrona, w zasadzie w granicach błędu pomiaru. Najczęściej w takich sytuacjach oceniam w stylu: 0,1 x 0,3 = 0,03 um.

- Na większych powierzchniach można spotkać obraz mieszany: na dużej powierzchni prążki równoległe a na pewnym obszarze plamy. Świadczy to o wklęsłości/ wypukłości miejscowej, np. wkłuciu. W skomplikowanych topografiach płaszczyzny najlepiej może sprawdzić się metoda z linią przecinającą.

Jest to dość wymagające, bo prążki wyglądają tak samo dla górki (wypukłość) i dołka (wklęsłość). Aby to rozróżnić, zastosuj prosty test:
Jak rozróżnić wadę wklęsłą od wypukłej?
- Delikatnie naciśnij palcem krawędź płytki interferencyjnej (w miejscu, gdzie „klin powietrzny” jest najgrubszy). Obserwuj, jak zachowują się prążki:
- Powierzchnia WYPUKŁA (górka): Płytka opiera się na środku – wierzchołku. Prążki zakrzywiają się w kierunku linii styku płytki z przedmiotem
- Powierzchnia WKLĘSŁA (dołek): Płytka opiera się na krawędziach. Prążki zakrzywiają się w kierunku „od” linii styku płytki z przedmiotem.
To właśnie dlatego najlepsza ocena zachodzi nie w sytuacji przywarcia płytki do powierzchni, a wtedy, gdy zachowujemy minimalny kąt.
Zwróćcie uwagę na pewne ułatwiające życie wnioski:
- skoro 1 prążek to 0,3 mikrona, to gdy sprawdzamy mikrometr możemy znaleźć maksymalnie 2 pełne prążki, gdyż trzeci dałby 0,9 mikrona i przekroczenie wymagania. Każda inna sytuacja, w tym obraz równoległy to spełnienie wymagania. Można więc na wewnętrzne potrzeby wprowadzić prostą ocenę OK/NOK.
- prążki równoległe to generalnie płaszczyzna o małej odchyłce, nieprzekraczającej 0,3 mikrona.
Na koniec raz jeszcze podkreślę znaczenie kątowego ułożenia płytki do badanej powierzchni. Jest to kluczowe zwłaszcza przy powierzchniach o niewielkiej odchyłce i równoległe ułożenie płaszczyzn w tym przypadku może dać fałszywy wynik w postaci braku prążków!
Ćwiczenie dla mistrzów: wyznaczenie różnicy wysokości dwóch płytek wzorcowych płytką interferencyjną
Ciekawym zastosowaniem metody jest porównywanie wymiaru dwóch płytek wzorcowych. Jako że różnica wysokości między nimi jest niewielka, można posłużyć się płytką szklaną w celu uzyskania obrazu prążków na połączonych powierzchniach…

Na koniec
I tak oto dobrnęliśmy do końca. Wiem, że zrozumienie podstaw metody zahacza mocno o poważną naukę, ale nie to jest najważniejsze. Ważne aby umieć zastosować ją w praktyce, a to po krótkiej wprawie staje się intuicyjne i zwyczajnie przyjemne. Tej i innych warsztatowych metod niezmiennie uczę na moich szkoleniach z wzorcowania i pomiarów, na które serdecznie zapraszam!














Opublikuj komentarz
Musisz się zalogować, aby móc dodać komentarz.