O wpływie temperatury na wyniki pomiarów długości każdy szanujący się pomiarowiec wie. Wszyscy wiedzą też, że mierzyć powinno się w 20 stopniach Celsiusza. Ale skąd dokładnie to wynika? Czy temat daje się zamknąć w stwierdzeniu, że wraz ze wzrostem temperatury wymiar zwiększa się? I czy na pewno rygorystyczne trzymanie się mitycznych 20 stopni jest zawsze bezwzględnie wymagane? Sprawdzamy jaki wkład w naszą codzienną pracę ma poprawka temperaturowa.

Temperatura odniesienia

Norma PN-EN ISO 1:2016 – Specyfikacje geometrii wyrobów (GPS) . Normalna temperatura odniesienia dla specyfikacji właściwości geometrycznych i wymiarowych, należy do wybitnie treściwych dokumentów o fundamentalnym znaczeniu ustalając temperaturę odniesienia na wartość 20ºC.

Temperatura ta powinna być traktowana jako ta, w której wyroby czy narzędzia powinny być weryfikowane pod kątem wymiarowym, a więc i na etapie projektowania zakładać należy, że wymiary nominalne osiągnięte powinny zostać przy tej właśnie temperaturze materiału.

Pamiętajmy, że mówimy tu o temperaturze materiału, a nie otoczenia. Nie ma zatem w normie wyspecyfikowanego przedziału temperatury odniesienia, a jedynie pożądana jej wartość.

Rozszerzalność cieplna i współczynnik rozszerzalności cieplnej

Rozszerzalność cieplna (liniowa bądź objętościowa) to właściwość fizyczna ciał polegająca na tym, że zwiększają one swoją długość (lub objętość) w miarę wzrostu temperatury. Na nasze potrzeby przyjmiemy, że zmiana długości jest proporcjonalna do zmiany temperatury. To, jak bardzo dany materiał jest „podatny” na wpływ temperatury, opisuje parametr zwany współczynnikiem rozszerzalności cieplnej. Poniższa tabela podaje wartości współczynników rozszerzalności dla najczęściej spotykanych materiałów. Skupiam się jedynie na materiałach istotnych z punktu widzenia praktyki pomiarowej, stąd zainteresowanych tematem szerzej odsyłam do innych źródeł.

MATERIAŁ	WARTOŚĆ WSPÓŁCZYNNIKA x 10-6 [1/ºC]
Stal zwykła niskostopowa	11,5 +/-2
Stal na płytki wzorcowe	11,5 +/-1
Stal na suwmiarki i mikrometry	11,5 +/-2
Szkło (wzorce inkrementalne, ZEISS)	10,8 +/-0,5
Szkło (wzorce inkrementalne, HEIDENHEIN)	8 +/-0,5
Węglik spiekany (wolfram)	5 +/-1
Zyrkon (ceramika, MAHR)	9,5 +/-1
Zerodur (ceramika)	0 +/-0,05

Znając współczynnik rozszerzalności liniowej oraz aktualną temperaturę obiektu, możemy wyznaczyć o ile zmienił się jego wymiar wraz ze zmianą temperatury. Zastosujemy wzór:

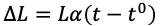
gdzie:

∆L – zmiana długości, L – długość początkowa, α – współczynnik rozszerzalności cieplnej, t – temperatura końcowa, t0 – temperatura początkowa

Co z tego wynika?

Eksperymentując z powyższym, możemy zauważyć że:

Płytka wzorcowa stalowa o długości 100 mm rozszerza lub kurczy się o ok. 1 µm na każdy 1ºC.

Odpowiada to ok. 10% przedziału tolerancji dla mikrometru zewnętrznego w tym zakresie według normy DIN 863, stanowi więc znaczne obciążenie dla naszej wyjściowej niepewności pomiaru. W przypadku suwmiarki wg DIN 862 (ISO 13385) w tym zakresie mamy dopuszczalne +/- 0,02 mm, a więc przedział 40 µm, zatem nasza zmiana długości to raptem 2,5%. Jednakże wyciągnięcie wniosku o niewielkim wpływie temperatury na wzorcowanie mniej dokładnych przyrządów jest zdecydowanie przedwczesne…

Stabilizacja temperatury

Aby uściślić nasze rozważania musimy poczynić kilka założeń. Po pierwsze – wartość, którą chcemy zmierzyć (menzurand) cały czas się zmienia. Jeśli nasz obiekt pomiaru przeniesiemy do ośrodka o innej temperaturze (będzie to obiekt np. świeżo po obróbce lub transporcie), jego wymiar będzie się zmieniał do momentu, aż jego temperatura zbliży się do temperatury otoczenia.

Przyjmuje się, że dla materiałów zbliżonych do stali czas stabilizacji temperatury przed rozpoczęciem pomiaru powinien wynieść co najmniej 3h.

Jak być może zwróciliście uwagę, współczynniki rozszerzalności podane wyżej, wyrażone są jako przedział (+/- x). Mogą zatem różnić się od siebie, a zmienność ta powinna zostać uwzględniona w budżecie niepewności pomiaru. W związku z niepewnością wynikającą z różnic współczynników rozszerzalności cieplnej, nawet przy zachowaniu odpowiednio długiego czasu stabilizacji (wyrównywania temperatur obiektu i przyrządu), wartość zmienności długości nigdy nie będzie równa zero.

Nadrzędnym celem stabilizowania temperatury jest zminimalizowanie różnicy temperatur obiektu mierzonego i przyrządu pomiarowego. Różnica ta ma decydujący wpływ na wartość błędu temperaturowego.

Poprawka temperaturowa

Jak wiemy poprawka przyjmuje wartość wyznaczonego błędu, ale z przeciwnym znakiem, co pozwala na usunięcie błędu z surowego wyniku pomiaru. Błąd temperaturowy obliczymy ze wzoru:

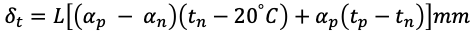
δt – błąd temperaturowy, L – długość mierzona, αp  – współczynnik rozszerzalności cielnej obiektu mierzonego, αn – współczynnik rozszerzalności cieplnej przyrządu, tn – temperatura przyrządu, tp – temperatura obiektu.

Poprawka temperaturowa zatem przyjmuje postać: -δt

Niepewność wyznaczenia poprawki

Wskazaliśmy już, że jednym ze źródeł niepewności wyznaczenia poprawki temperaturowej są różnice i niepewność wyznaczenia współczynnika rozszerzalności. Kolejnym źródłem niepewności będzie niepewność wyznaczenia temperatur przyrządu i obiektu.

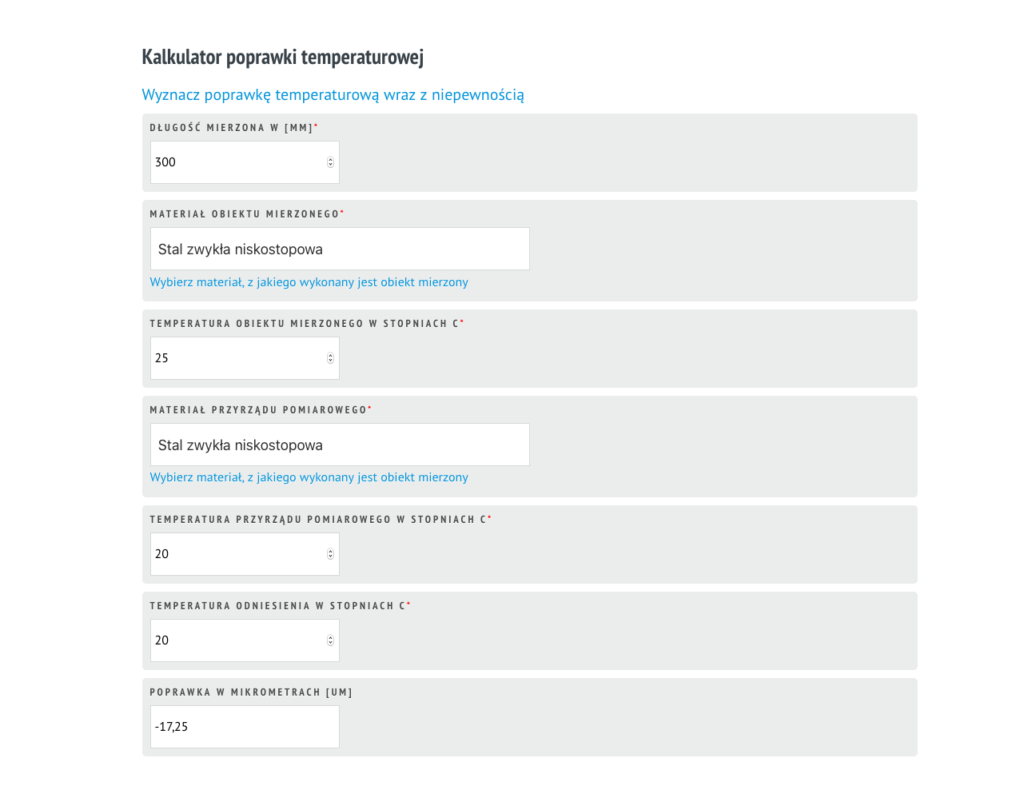
Poprawka temperaturowa – kalkulator

Przy okazji pisania niniejszego wpisu próbowałem odnaleźć w internecie prosty kalkulator pozwalający na wyznaczenie poprawki temperaturowej przy wprowadzeniu zmiennych w postaci materiału i temperatury obiektu mierzonego i przyrządu. Ponieważ nie udało mi się takiego narzędzia odnaleźć, stworzyłem własny, który dostępny jest pod podanym niżej adresem. Mam nadzieję, że okaże się przydatny, a ja na pewno niebawem rozbuduję go o niepewność pomiaru wyznaczania poprawki. Zapraszam do korzystania.

https://metrica.com.pl/poprawka-temperaturowa/

Co dalej?

Zachęcam do eksperymentowania i wykonania własnych obliczeń dla realnych i hipotetycznych sytuacji, bo w ten właśnie sposób nabieramy niezbędnej wyobraźni i wiedzy. W kolejnej części wpisu sprowadzimy temat do warstwy praktycznej i odniesiemy liczby do codziennej pracy metrologa.